Programiranje u fizici
- 7. DEO -
U ovom delu se će biti demonstrirano kako se primenom Ojlerovog metoda mogu aproksimativno rešiti diferencijalne jednačine drugog reda. Biće konkretno predstavljeni modeli Linearnog Harmonijskog Oscilatora (LHO), bez i sa prigušenjem, RLC kolo, oscilovanje matematičkog klatna u vakuumu i vazduhu.
U ovom delu videće se i ograničenje Ojlerovog metoda kada se radi o modelima koji opisuju oscilatorno kretanje i/ili kretanje koje se brzo menja. Zbog toga će biti uveden i Ojlerov-Kromerov algoritam, koji se dobija lakom modifikacijom Ojlerovog metoda.
1. Linearni harmonijski oscilator (bez prigušenja)
Linearni harmonijski oscilator (LHO) je jedan od najpoznatijih i najznačajnijih modela u fizici. Šematski prikaz LHO je dat na slici 7.1.
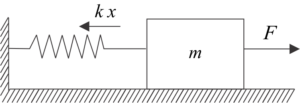
Šema prikazana na slici predstavlja idealni LHO ili LHO bez prigušenja. U tom slučaju se podrazumeva da telo mase \(m\) osciluje bez ikakvih prepreka u vidu sile trenja sa podlogom na kojoj se nalazi, ili neke dodatne sile koja bi delovala u smeru suprotnom od smera kretanja.
Do kretanja pomenutog tela dolazi zbog dejstva elastične sile opruge, za koju se zna da ima oblik:
$$F = -k\cdot x$$
Sila \(F\) dovodi do istezanja opruge, a znak minus se naravno javlja zbog toga što elastična sila deluje suprotno od smera kretanja tela. Izražavanjem sile preko drugog Njutnovog zakona dolazi se do sledeće diferencijalne jednačine:
$$m\cdot \frac{d^2 x}{dt^2}=-\frac{k}{m} \cdot x$$
U literaturi se najčešće sreće malo drugačiji napisan oblik poslednje jednačine:
$$m\cdot \frac{d^2 x}{dt^2}+\frac{k}{m} \cdot x=0$$
Dobijena diferencijalna jednačina je jedna od najpoznatijih jednačina u fizici, a njeno egzaktno rešenje je:
\[ \cos(\frac{a}{b} \cdot \theta + \phi) = \cos \theta \cos \phi
– \sin \theta \sin \phi \]
$$x(t) = A \sin(a)$$
$$x(t) = A \cdot \sin(\sqrt{\frac{k}{m} \cdot t) + B \cdot \cos(\sqrt{\frac{k}{m} \cdot t})$$
U poslednjoj jednačini se često uvede smena: \(\omega=\sqrt{k/m}\), pa se dolazi do sledeće jednačine:
$$x(t) = A \cdot \sin(\omega \cdot t) + B \cdot \cos(\omega \cdot t)$$
Ideja za rešavanje diferencijalne jednačine (2) jeste uvođenje smene, kako bi se redukovao stepen diferencijalne jednačine. Uvođenjem sledeće smene:
$$\frac{dx}{dt}=v$$
prelazi se sa diferencijalne jednačine drugog reda, date jednačinom (2), na sistem diferencijalnih jednačina prvog reda:
$$\frac{dx}{dt}=v$$
$$\frac{dv}{dt}=-\frac{k}{m} \cdot x$$
Zatim se dobijene dve diferencijalne jednačine prvog reda aproksimativno rešavaju primenom Ojlerovog algoritma na isti način kao i do sada. Odgovarajući kod je dat u primeru LHO sa sledećim parametrima: \(m=1 \: \mathrm{kg}\) , \(k=1\) i \(x_0= 2 \: \mathrm{m}\).
Primer 7.1. – Primena Ojlerovog metoda za rešavanje diferencijalne jednačine LHO
Dati program za primer 7.1. poredi egzaktno i aproksimativno rešenje. Vidi se da Ojlerov metod ovde ne daje fizički adekvatan rezultat, jer amplituda sa svakom oscilacijom raste. Ovo naravno nije moguće, jer sistem ne dobija dodatnu energiju, pa nema na račun čega da se povećava amplituda. Ovo je nedostatak Ojlerovog metoda kada se primenjuje na modele sa oscilatornim ponašanjem i “brzim” promenama vrednosti.
Situacija u vezi primene Ojlerovog metoda u pomenutim slučajevima se može poboljšati, ali samo donekle, povećanjem vrednosti \(n\), odnosno smanjenjem koraka \(h\). Ovo se ne smatra dobrim rešenjem, jer nikako ne možemo znati koje su dobre početne vrednosti ovog parametra.
Međutim, uvođenjem male korekcije u algoritam, dobija se fizički korektno rešenje. Naime, ukoliko se u for petlji traži da se računanje brzine (linija 33 u primeru 7.1.) vrši na osnovu nove vrednosti \(x\), a ne stare, dobijaju se fizički korektan rezultat. Ovaj metod se naziva Ojler-Kromerov metod, i demonstriran je u sledećem primeru (u odnosu na prethodni kod, razlikuje se samo u pomenutoj liniji 33).
Primer 7.2. – Primena Ojler-Kromerovog metoda za rešavanje diferencijalne jednačine LHO
Kao što se može videti, slaganje između aproksimativnog i egzaktnog rešenja je odlično, čak iako se vrednost \(n\) višestruko smanji.
2. Linearni harmonijski oscilator sa prigušenjem
gde je \(c\) konstanta prigušenja. Na isti način kao i kod idealnog LHO, dolazi se do sledeće diferencijalne jednačine koja opisuje prigušeni LHO:
$$\frac{dv}{dt}=-\frac{c}{m} \cdot v -\frac{k}{m} \cdot x$$
Sada se na isti način kao i kod idealnog LHO može pisati program kojim se aproksimativno modeluje prigušeni LHO. Pre nego što se predstavi primer u kojem se preko Ojler-Kromerovog metoda rešava pomenuti sistem diferencijalnih jednačina, treba napomenuti da vrednost konstante prigušenja diktira tip prigušenog oscilovanja. Konkretno, vrednost konstante prigušenja određuje vrednost diskriminante:
$$D=c^2-4mk$$
koja se pojavljuje kod rešavanja homogenih diferencijalnih jednačina drugog reda, kakva je jednačina (12). U tom smislu, različite vrednosti konstante prigušenja mogu dovesti do sledećih tipova prigušenog oscilovanja LHO:
- kritično prigušeno (\(D=0\)),
- kvaziperiodično (\(D<0\)) i
- aperiodično (\(D>0\)).
U primeru koji sledi, 7.3., predstavljen je program u kojem se pomoću Ojler-Kromerovog metoda rešava sistem jednačina (jednačine (13) i (14)) pri čemu su vrednost parametara iste kao i u prethodnom primeru, s tim što je konstanta prigušenja \(c=2\). Čitaocima se ostavlja kao vežba da definišu različite vrednosti konstante prigušenja, prema jednačini diskriminante (15), kako bi se dobili grafici koji opisuju različite tipove prigušenog oscilovanja.
Primer 7.3. – Program za rešavanje diferencijalne jednačine prigušenog LHO
3. Matematičko klatno
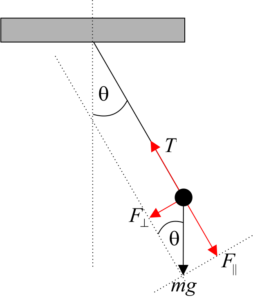
U najjednostavnijem slučaju, kod modela matematičkog klatna podrazumeva se da je mala kuglica okačena o nerastegljivu nit. Sa slike 7.2. se vidi da do kretanja dolazi usled dejstva jedne od komponenti sile Zemljine teže:
$$F_R=F_{\perp}=-mg \sin\theta$$
Ako se rezultujuća sila napiše preko drugog NJutnovog zakona, dobija se sledeća jednačina:
$$m\cdot \frac{d^2s}{dt^2}=-mg \sin\theta$$
gde je \(ds\) element pređenog puta po kružnici. Za infinitezimalno malu vrednost pređenog puta po kružnici, \(ds\), pređeni put se može izrazitikao \(s=l \cdot \theta\), pa se dobija:
$$m\cdot \frac{d^2 (l\cdot \theta)}{dt^2}=-mg \sin\theta$$
Pošto se menja samo ugao, dobija se sledeća jednačina:
$$l\cdot \frac{d^2\theta}{dt^2}=-g \sin\theta$$
odnosno
$$\frac{d^2\theta}{dt^2}=-\frac{g}{l} \sin\theta$$
Ostaje da se iskoristi još jedna aproksimacija. U slučaju malih oscilacija, važi da je \(\sin(\theta) \approx \theta \), pa konačno sledi:
$$\frac{d^2\theta}{dt^2}=-\frac{g}{l} \theta$$
U literaturi se češće sreće malo drugačiji oblik:
$$\frac{d^2\theta}{dt^2} +\frac{g}{l} \theta=0$$
Dobijena diferencijalna jednačina opisuje oscilovanje matematičkog klatna i ako se uporedi sa diferencijalnom jednačinom koja opisuje LHO, vidi se da je matematički oblik identičan, pa su ova dva modela analogna.
Diferencijalna jednačina (21) se na isti način kao i kod LHO može rešiti aproksimativno upotrebom Ojler-Kromerovog metoda. Prvi korak je naravno uvođenje smene, nakon čega se dobija sistem diferencijalnih jednačina prvog reda:
$$\frac{d\theta}{dt}=\omega$$
$$\frac{d\omega}{dt}=-\frac{g}{l}\theta$$
Ideja za rešenje dobijenog sistema je identična kao i kod LHO, što će biti demonstrirano sledećim primerom gde su vrednosti parametara sledeće: \(g=10 \: \mathrm{m/s^2}\), \(l = 1,6 \: \mathrm{m}\), \(\theta_0 = 0,3 \: \mathrm{rad}\), \(t_0=0 \: \mathrm{s}\), \(t_f = 20 \: \mathrm{s}\)
Primer 7.4. – Program za rešavanje diferencijalne jednačine matematičkog klatna u vakuumu Ojler-Kromerovom metodom
4. Prigušeno matematičko klatno
Primer 7.5. – Prigušeno matematičko klatno (kliknuti na dugme “Code” da se dobije rešenje)